Annotated Excerpts from: ‘Mathematics Education in India, 2012, Chapter-3 (author: D. Senthil Babu)

All excerpts are italicized. Emphasis in bold is ours.

Pedagogy

D. Senthil Babu notes “Along with diversity in curriculum, the pathshalas seemed to share a culture of pedagogy grounded in a form of memory very different from the modern associations of memory with rote or mechanical mode. This could be characterized as recollective memory where memory practices constituted a distinct mode of learning and not merely aids to learning…”

To comprehend how incredibly effective and successful the indigenous approach to teaching Ganita was:

“Learning arithmetic in this mode cultivated computational abilities that often attracted attention. A historical perspective on mathematics education in India among visitors so much so that it became common to characterize Indians as having a natural proclivity towards computation: “the natives of India are remarkable for the facility with which they acquire the mathematics; and indeed they excel in anything in which figures or numbers are concerned. .. the power which the little schoolboys display in mental arithmetic is quite astonishing to the European” (Rhenius, 1841, p. 269-70). Jean Baptiste Tavernier traveling in 1665 mentions the quick abilities of Indians to sum and perform mental calculations. …The East India Company offered rewards (twenty pounds!) to
its soldiers if they would learn arithmetic from the natives (Sarma, 1997).”

On the use of numerical tables:

“The Bombay Gazetteer mentioned, “… boy commits to memory a number of very elaborate tables. These tables of which there are no fewer than twenty contain among  others two sets for whole numbers, one table of units up to ten multiplied to as high as forty times; the other for numbers eleven to twenty multiplied by eleven to twenty times. There are fraction tables giving the results of multiplying and into units from one to one hundred; interest tables showing the monthly rate of one percent on sums from Re. 1 to Rs. 1000, the amount due for each quarter of a month; tables of squares of all numbers  from one to 100 and a set of technical rules for fi nding the price of a part from the price of the whole” (Sarma, 1997).”

On the familiarity with Algebra (that originated in India)

“Lal Behari Dey writing about the life of the Bengali peasant writes, “the village school master was the first mathematician of the village. … acquainted with the elements of vijaganita or Algebra”.

On the democratization and dissemination of mathematical knowledge to all classes of the society and the different regions of India using a suitably customized approach:

“there are four distinct aspects that further point towards a dynamic culture of engagement with transmission of mathematical knowledge in the Indian past. They are i) math tables which could have been manuals used in the pathshalas in the different regional languages ii) compilations of mathematical techniques in regional languages iii) various forms of problem posing and problem solving in popular consciousness and iv) certain kinds of practices inherent to various occupational or artisanal groups.”

Also well known in the story of Ibn Sina (Avicenna), the greatest Persian and Islamic scholar of his era (circa 1000 CE), who learned Ganita from the Indian vegetable vendor. Clearly, the Indian approach to education and knowledge was not one where it remained the preserve of an elite few, but was available to everybody.

The Thinnai (Tinnai) school approach to Ganita in Tamil Nadu

You will often hear Tamizh Grandmas and Grandpas tell you that they were taught math in a much better way in their village schools compared to kids today. They were not wrong.

Number series

“Every number in the primary number series would be memorized in a particular order,
in the pattern of integrating the sound of the number name, visual recognition of the
symbol, loud recital and writing, with concurrent testing at each level by the monitor
or the teacher. This elementary number series consisted of both whole numbers and an
extensive system of fractions in the Tamil system.”

Addition

“There were separate sessions in the tinnai routine, where the children would stand up and recite the entire series in unison, loudly in front of the teacher, one series after the other, repeatedly, day after day till the logic of addition as the basis of number organization is cognitively internalized along with the process of building memory registers for the numbers in a particular order. This would mark the the memory learning of the elementary number series in Tamil called the Ponnilakkam, (pon = gold; ilakkam = number place, in the literal sense), denoting a particular order of numbers, as quantities. Next in line is the Nellilakkam (nel = paddy; ilakkam – number place) which is a number series that takes the units of Tamil volumetric measures as numbers and proceeds along similar lines as that of the Ponnilakkam”

Multiplication

“Followed by this was the learning of the Tamil multiplication table book called the
Encuvati. The Encuvati is a compilation of several kinds of multiplication tables.
All the numbers learnt during the course of Ponnilakkam and Nellilakkam would be
subjected to multiplication with each other, to yield an entire set of tables, that were
to be committed to memory.”

Problem Solving

“The Encuvati learning sessions involved regular afternoon sessions of problem posing and solving in the tinnai schools. Here, recollective memory would have to score well in an algorithmic context. The students carried back problems to their homes, where problem solving happened in a non-institutional context, entirely orally to aid the process of strengthening the cognitive apparatus of associative memory. The next morning, the results were collected and discussed.”

“In a social sense, all such arithmetic representation with embedded cognitive aspirations, are characterized by a yearning to enable a person to be in control of a situation, to plan, estimate, assess and anticipate”

Popularizing Ganitha

“It is still not uncommon to find in several parts of the country, especially in rural areas, the circulation of mathematical problems as riddles and aphorisms among the people. The correspondence between what exists in the memory of the people, in certain realms of popular consciousness and their variants in the prosodic form recorded in texts is yet to be studied. However it does point to a common shared culture of problem solving among people. Such problems are often termed as recreational problems…”

Ganitha in the workplace

“Another realm that testifies to forms of transmission in the indigenous tradition is the one through work, involving artisanal communities and specialized craftsmen like carpenters, sculptors, goldsmiths, etc. Though the practice of apprenticeship in the various crafts and artisanal work varies with the nature of the profession and the community, the nature of the mathematical engagement in such work involves learning on the job. There are several texts which are like manuals for certain crafts both in the regional language traditions as well as in Sanskrit, from the past”

How the Thinnai Pedagogy was digested by British Missionaries and re-exported back to India

In this section, we map the data provided in the reference to the five stages of the U-turn model described by Rajiv Malhotra in his 2006 Lecture at Lady Sri Ram College, New Delhi. The stages are numbered in blue text below, corresponding to the description in the picture [copyright: Rajiv Malhotra].

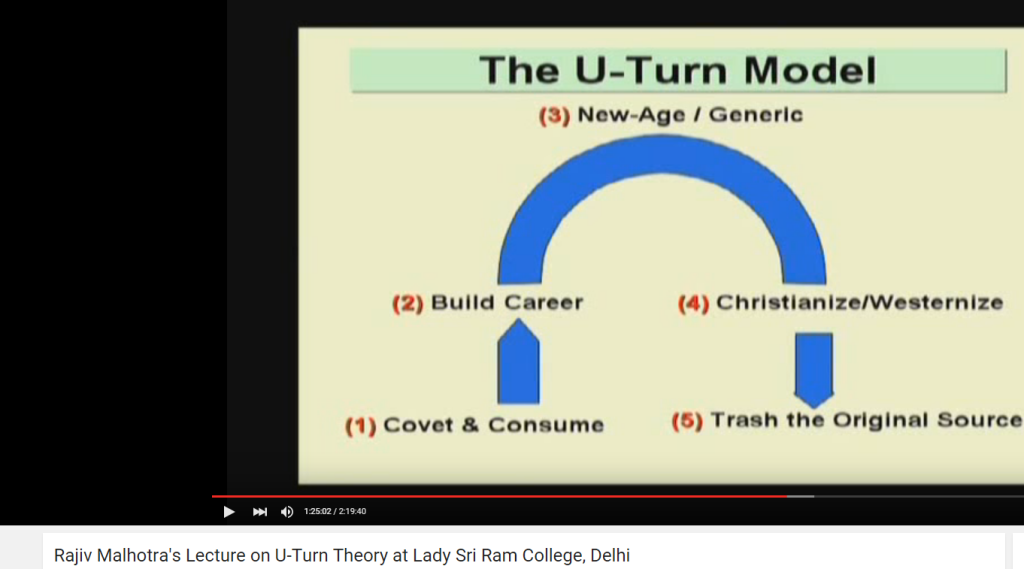“One of the most ironic aspects of this legacy unfolded in the early nineteenth century when the colonial project in the name of dislodging mechanical memory from the pathshala practice did exactly the reverse by bringing it right in to the centre of learning.”

“Here is the story of a system of pedagogic knowledge, which traveled from India, became one of the primary means to popularize elementary education in England, and came back to India, all along, going through continuous attempts at modification and improvement. This was called the Madras System of Education..”

Rev. Bell and Mr. Lancaster

“Rev. Andrew Bell was the company chaplain in the Egmore Male Asylum in Madras in South India, during 1789-96. During his tenure, he encountered, or rather, discovered the tinnai pedagogy during one of his morning rides. [stage-1]

Bell practiced his experiments in the Egmore asylum till he left for England in 1797,
where he published his book on the Madras system in the same year [stage 2]. His arithmetic
pedagogy, as spelt out in his book had very close resemblance to the Encuvati mode of
learning in the tinnai schools”

Even though the available accounts in England make it out as a dramatic discovery of writing on sand (for reasons of economy) and for its monitorial system [stage 3]., in effect, Rev. Bell did two things:
• The actual working of the tinnai pedagogy was reframed into a set of principles
based on Christian value system [stage 4]

• Internally, the memory mode of learning in the tinnai, using mutual instruction was reconstructed with respect to reading, writing and arithmetic, the three R’s, as perceived in England.”

Bell and Lancastar become famous in England

“There ensued a major controversy between Bell and Joseph Lancaster, a dissenter and a Quaker, who claimed to have invented the monitorial system of education independently
The entire affair turned out be messy and engaged several levels of arbitration, including the Church of England and the Princess of Wales”

“Both Bell and Lancaster provided a major impetus to the spread of popular education in England, where education had been confined to the classical learning in the public schools and the two universities for the elite whereas the poor went to the Sunday schools, which were conceived as a means to counter the emerging radicalism of the working class.”

The Pizza Effect

Next, we see how the Thinnai system after being studied, and then ‘digested’ into the “monitorial system of English education” using missionary values, is re-exported back to India within 30 years.

“In the South, Bishop Middleton started a school under the Bell model in 1819, followed by Fr. Rhenius of the CMS in the schools of Tirunelveli around the same time. The localizing of the Bell pedagogy in South India through the missionaries, brought up a scenario where within the same Tamil missionary institution, one had the Bell system in operation, with Tamil schoolmasters; and in other sections, a different Tamil schoolmaster would be teaching Tamil arithmetic of the Encuvati mode, using palm leaves.”

Next comes the appropriation and finally, the total digestion of Pathashalas, and the attempted destruction of the indigenous methods.

“The dominant story however from the mid nineteenth century onward was the consistent
attempts by the colonial administration to convert the pathshalas of the various regions
into modern schools, apart from parallel attempts to institute their own set of institutions
teaching European sciences.”

“The traditional arithmetic now got assimilated into the official curriculum as ‘mental arithmetic’ along with slate centered practice of learning the four basic arithmetic operations and the rule of three. The tables of the Encuvati now became part of the new textbooks including the conversion tables of the various weights and measures into the modern English measures, while the use of Tamil numerical notation was entirely done away with. Rechristened now as ‘bazaar mathematics’, [stage-5] mental arithmetic became a regular adjunct to the rule based problem solving in practice and reduction. It was not recollective memory as the very mode of learning.”

Summary of the colonial encounter

“The encounter highlights the inherent contradictions of the colonial project. The resilience of indigenous institutions was based on a social resource, namely the public perception of what a relevant curriculum should be in the local school. Training in arithmetic was considered essential for participation in local economic transactions. Set against this was the colonial empire building exercise with its agenda of homogenization, which set out to counter and liberate the pathshala curriculum from its functional ethos, but the pathshala functionality refused to yield. What this left behind was a legacy of mechanical memory as the dominant mode of learning arithmetic, whereas arithmetic was not a goal of the pathshala but computational ability in context“